How do I study rotational dynamics for the JEE?

Physics describes the laws and equations which governs nature and natural phenomena. Physics primary focus is the study of motion.
Rotational motion can be seen in almost everything around us. Some common day-to-day examples are a machine, celestial bodies, football, fun games in amusement parks etc.
Objects rotate on an axis. All the particles and mass center do not have identical motions. But all the particles of the body have identical motion.
Rotational Kinematics
In rotational kinematics, we will see the relation between kinematical parameters of rotation.
Axis of rotation
A rigid body of any shape which rotates about a fixed axis is called an axis of rotation or rotation.


Types of motion involving rotation
- Pure rotation or rotation about a fixed axis
- Combined translational and rotational motion or rotation about an axis of rotation
Rotation about a fixed axis
Rotation about a fixed axis can be best explained with the examples of rotation of the planet Earth, rotation of a ceiling fan, rotation of hour and minute hands in analog clocks.
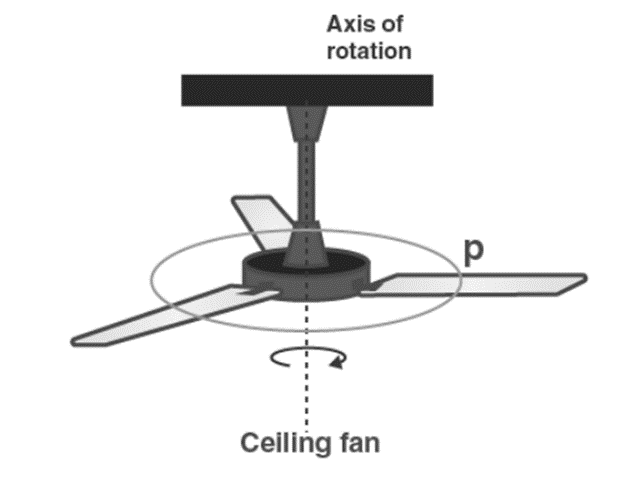

Rotation about an axis of rotation
Example of rotation about an axis of rotation is rolling. In rotational physics, it is applied in the rolling of wheels and wheels like objects such as automobiles and other rolling wheels.
The motion of rolling occurs due to the combination of both translational and rotational motion of a round-shaped body placed on a surface. When a body starts to roll, then all the particles of the body have two velocities. One happens due to the rotational motion and the other happens due to the translational motion of the center of mass. The result is the vector sum of both velocities at all particles.

Kinetic energy of rotation
The blades of a table saw machine and the blades of a fan have kinetic energy due to the rotation. When the familiar equation is applied to the saw machine as a whole, it will give kinetic energy of its center of mass only, which is equal to zero.

The right approach
Let us take the saw machine or any rotating rigid body having a collection of particles at different speeds. To find the rotational kinetic energy of the whole body, the kinetic energy of the particles is summed up.
When m1, m2,…, are the masses of the constituent particles moving on circular paths with radii r1, r2,…, having velocities v1, v2,…, then the kinetic energy of the body is represented by;

What is Torque?
Torque can be defined as a rotational analogue of force and shows the tendency of a force which is applied to an object that causes the object to rotate about a given point.
When we open a door, we apply force on the doorknob which is located far from the hinges of the door. When we try to apply the force near the hinge line than the knob, or at any other angle other than 90degree to the plane of the door, then greater force must be applied than the former to rotate the door.

In order to find how the applied force causes the rotation of the body about an axis, we break the Force (F) into two parts. The tangential component is perpendicular to r which causes rotation whereas the radial component does not cause rotation because it is along the line which intersects with the axis or pivot point.
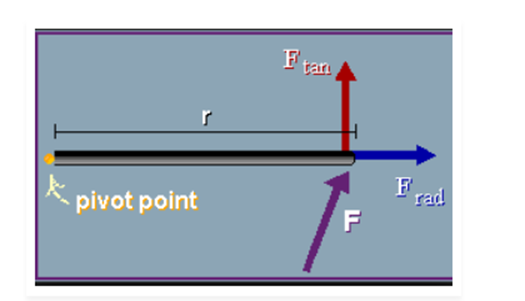
The ability to rotate the body is dependent on the magnitude of the tangential component and on how far from the axis the force is applied.
Mathematically, it can be expressed as

Stability of the object
- When the rotational inertia of the object is greater, then the object is more stable because it becomes difficult to move.
- The stability of an object is also dependent on the torque produced by its weight. When the torques are larger and the mass is from COM, then more force is needed to change the stability.
- When the rotation of an object is greater, then the object is more stable.
Newton’s second law of motion
When the net torque which acts on the body about any inertial axis is and the moment of inertia about that axis is l, then the angular acceleration of the body is shown by the relation:

Rotational equilibrium
When the total external force acting on a body is zero, then the center of mass of the body remains in a state of equilibrium. This is derived from the equation F = Ma.
Likewise, when the total external torque acting on the body is zero, then the body remains in a state of rotational equilibrium. This is derived from the equation . Hence, a body which is in a state of rotational equilibrium must be in rest or rotation with constant angular velocity.
Important question, solve this: A wheel of radius 1 m rolls forward half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially on contact with the ground is?
Also check: olivia rodrigo


